Notebook source code:
examples/bistable/bistable.ipynb
Run the notebook yourself on binder

Bistable gene-regulatory networks¶
Model definition¶
We consider the piecewise linear system defined in Filippov sense as in Augier and Yabo (2021). In synthetic biology, this model can represent a genetic toggle switch, a synthetic regulatory network designed by Gardner et al. (2000) in the bacteria E. coli through two genes lacI and tetR mutually repressing each other. Dynamics is given by
where for \(j\in \{1,2\}\), \(x_j\in \mathbb{R}\), and for \(\theta\in \mathbb{R}\), \(s^{-}(\cdot,\theta):\mathbb{R}\to \mathbb{R}\) is such that
and the control \(u(\cdot) \in L^\infty ([0,t_f],[u_{\text{min}},u_{\text{max}}])\), with \(0<u_{\text{min}}<1 \leq u_{\text{max}}\). Such system is piecewise linear in \(\mathbb{R}^2\) and, in particular, is linear in the regular domains
The following image shows the dynamics for the open loop system (i.e. \(u \equiv 1\)):
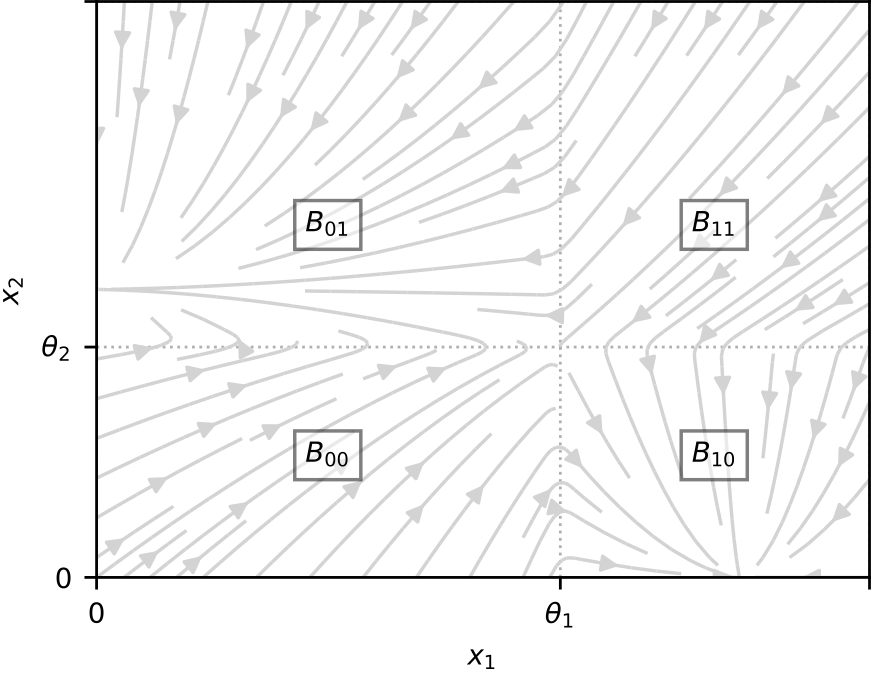
Time-optimal control problem¶
The optimal control problem involves minimizing the time of a state transfer from \(B_{10}\) to \(B_{01}\), and so is defined for the state \(x(t) = (x_1(t),x_2(t))\) as
with \(f(x)\) being the right-hand side of the system previously introduced.
Problem regularization¶
Bocop requires \(s^-\) to be regularized to a smooth function. We then define, for \(x\in \mathbb{R}\) and \(k\in \mathbb{N}\), the Hill function
which can approximate \(s^-\) for large values of \(k\) and, when \(k \rightarrow \infty\), meets
System parameters are fixed to \(\gamma_1 = 1.2\), \(\gamma_2 = 2\), \(\theta_1 = 0.6\), \(\theta_2 = 0.4\) and \(k_1 = k_2 = 1\), and control bounds are set to \(u_{min}=0.5\) and \(u_{max}=1.5\). Initial conditions are set to \(x_1(0) = 0.8\), \(x_2(0)=0.3\) and \(x_2(t_f) = 0.7\). The parameter \(k\) of the Hill function is set to \(k = 200\).
[1]:
!pygmentize problem.cpp
// +++DRAFT+++ This class implements the OCP functions
// It derives from the generic class bocop3OCPBase
// OCP functions are defined with templates since they will be called
// from both the NLP solver (double arguments) and AD tool (ad_double arguments)
//#pragma once
#include <OCP.h>
template <typename Variable>
void OCP::finalCost(double initial_time, double final_time, const Variable *initial_state, const Variable *final_state, const Variable *parameters, const double *constants, Variable &final_cost)
{
// Minimize final time
final_cost = initial_state[2];
}
template <typename Variable>
void OCP::dynamics(double time, const Variable *state, const Variable *control, const Variable *parameters, const double *constants, Variable *state_dynamics)
{
Variable x1 = state[0];
Variable x2 = state[1];
Variable tf = state[2];
Variable u = control[0];
double g1 = constants[0];
double g2 = constants[1];
double t1 = constants[2];
double t2 = constants[3];
double k = constants[4];
Variable delta1 = pow(t2,k)/(pow(t2,k) + pow(x2,k)); // delta(x2,t2,k)
Variable delta2 = pow(t1,k)/(pow(t1,k) + pow(x1,k)); // delta(x1,t1,k)
state_dynamics[0] = -g1*x1 + u*delta1; // x1dot
state_dynamics[1] = -g2*x2 + u*delta2; // x2dot
state_dynamics[2] = 0; // tf (constant)
// Rescale the state
for (size_t i=0; i<2; i++)
state_dynamics[i] *= tf;
}
template <typename Variable>
void OCP::boundaryConditions(double initial_time, double final_time, const Variable *initial_state, const Variable *final_state, const Variable *parameters, const double *constants, Variable *boundary_conditions)
{
boundary_conditions[0] = initial_state[0]; // x1(0)
boundary_conditions[1] = initial_state[1]; // x2(0)
boundary_conditions[2] = final_state[0]; // x1(tf)
boundary_conditions[3] = final_state[1]; // x2(tf)
}
template <typename Variable>
void OCP::pathConstraints(double time, const Variable *state, const Variable *control, const Variable *parameters, const double *constants, Variable *path_constraints)
{}
void OCP::preProcessing()
{}
// ///////////////////////////////////////////////////////////////////
// explicit template instanciation for template functions, with double and double_ad
// +++ could be in an included separate file ?
// but needs to be done for aux functions too ? APPARENTLY NOT !
template void OCP::finalCost<double>(double initial_time, double final_time, const double *initial_state, const double *final_state, const double *parameters, const double *constants, double &final_cost);
template void OCP::dynamics<double>(double time, const double *state, const double *control, const double *parameters, const double *constants, double *state_dynamics);
template void OCP::boundaryConditions<double>(double initial_time, double final_time, const double *initial_state, const double *final_state, const double *parameters, const double *constants, double *boundary_conditions);
template void OCP::pathConstraints<double>(double time, const double *state, const double *control, const double *parameters, const double *constants, double *path_constraints);
template void OCP::finalCost<double_ad>(double initial_time, double final_time, const double_ad *initial_state, const double_ad *final_state, const double_ad *parameters, const double *constants, double_ad &final_cost);
template void OCP::dynamics<double_ad>(double time, const double_ad *state, const double_ad *control, const double_ad *parameters, const double *constants, double_ad *state_dynamics);
template void OCP::boundaryConditions<double_ad>(double initial_time, double final_time, const double_ad *initial_state, const double_ad *final_state, const double_ad *parameters, const double *constants, double_ad *boundary_conditions);
template void OCP::pathConstraints<double_ad>(double time, const double_ad *state, const double_ad *control, const double_ad *parameters, const double *constants, double_ad *path_constraints);
[2]:
%matplotlib inline
import bocop
[3]:
problem_path = "." # using local problem definition
bocop.build(problem_path, cmake_options = '-DCMAKE_CXX_COMPILER=g++')
[EXEC] > ['cmake -DCMAKE_BUILD_TYPE=Debug -DPROBLEM_DIR=/opt/ct-gallery/gallery/examples/bistable -DCPP_FILE=problem.cpp -DCMAKE_CXX_COMPILER=g++ /opt/ct-gallery/env/lib/python3.7/site-packages/bocop']
> -- The C compiler identification is GNU 7.5.0
> -- The CXX compiler identification is GNU 10.2.0
> -- Detecting C compiler ABI info
> -- Detecting C compiler ABI info - done
> -- Check for working C compiler: /opt/ct-gallery/env/bin/x86_64-conda-linux-gnu-cc - skipped
> -- Detecting C compile features
> -- Detecting C compile features - done
> -- Detecting CXX compiler ABI info
> -- Detecting CXX compiler ABI info - done
> -- Check for working CXX compiler: /usr/bin/g++ - skipped
> -- Detecting CXX compile features
> -- Detecting CXX compile features - done
> -- Problem path: /opt/ct-gallery/gallery/examples/bistable
> -- Using CPPAD found at /opt/ct-gallery/env/include/cppad/..
> -- Using IPOPT found at /opt/ct-gallery/env/lib/libipopt.so
> -- Found Python3: /opt/ct-gallery/env/bin/python3.7 (found version "3.7.8") found components: Interpreter Development Development.Module Development.Embed
> -- Found SWIG: /opt/ct-gallery/env/bin/swig (found suitable version "4.0.2", minimum required is "4")
> -- Build type: Debug
> -- Configuring done
> -- Generating done
> -- Build files have been written to: /opt/ct-gallery/gallery/examples/bistable/build
[DONE] > ['cmake -DCMAKE_BUILD_TYPE=Debug -DPROBLEM_DIR=/opt/ct-gallery/gallery/examples/bistable -DCPP_FILE=problem.cpp -DCMAKE_CXX_COMPILER=g++ /opt/ct-gallery/env/lib/python3.7/site-packages/bocop']
[EXEC] > make
> Scanning dependencies of target bocop
> [ 3%] Building CXX object src/CMakeFiles/bocop.dir/AD/dOCPCppAD.cpp.o
> [ 7%] Building CXX object src/CMakeFiles/bocop.dir/DOCP/dOCP.cpp.o
> [ 10%] Building CXX object src/CMakeFiles/bocop.dir/DOCP/dODE.cpp.o
> [ 14%] Building CXX object src/CMakeFiles/bocop.dir/DOCP/dControl.cpp.o
> [ 17%] Building CXX object src/CMakeFiles/bocop.dir/DOCP/dState.cpp.o
> [ 21%] Building CXX object src/CMakeFiles/bocop.dir/DOCP/solution.cpp.o
> [ 25%] Building CXX object src/CMakeFiles/bocop.dir/NLP/NLPSolverIpopt.cpp.o
> [ 28%] Building CXX object src/CMakeFiles/bocop.dir/OCP/OCP.cpp.o
> [ 32%] Building CXX object src/CMakeFiles/bocop.dir/tools/tools.cpp.o
> [ 35%] Building CXX object src/CMakeFiles/bocop.dir/tools/tools_interpolation.cpp.o
> [ 39%] Building CXX object src/CMakeFiles/bocop.dir/opt/ct-gallery/gallery/examples/bistable/problem.cpp.o
> [ 42%] Linking CXX shared library /opt/ct-gallery/gallery/examples/bistable/libbocop.so
> [ 42%] Built target bocop
> Scanning dependencies of target bocopwrapper_swig_compilation
> [ 46%] Swig compile /opt/ct-gallery/env/lib/python3.7/site-packages/bocop/src/bocopwrapper.i for python
> Language subdirectory: python
> Search paths:
> ./
> /opt/ct-gallery/env/include/python3.7m/
> AD/
> DOCP/
> NLP/
> OCP/
> tools/
> /opt/ct-gallery/env/include/cppad/../
> /opt/ct-gallery/env/include/coin/
> /opt/ct-gallery/env/include/python3.7m/
> /opt/ct-gallery/env/lib/python3.7/site-packages/bocop/src/AD/
> /opt/ct-gallery/env/lib/python3.7/site-packages/bocop/src/DOCP/
> /opt/ct-gallery/env/lib/python3.7/site-packages/bocop/src/NLP/
> /opt/ct-gallery/env/lib/python3.7/site-packages/bocop/src/OCP/
> /opt/ct-gallery/env/lib/python3.7/site-packages/bocop/src/tools/
> ./swig_lib/python/
> /opt/ct-gallery/env/share/swig/4.0.2/python/
> ./swig_lib/
> /opt/ct-gallery/env/share/swig/4.0.2/
> Preprocessing...
> Starting language-specific parse...
> Processing types...
> C++ analysis...
> Processing nested classes...
> Generating wrappers...
> [ 46%] Built target bocopwrapper_swig_compilation
> Scanning dependencies of target bocopwrapper
> [ 50%] Building CXX object src/CMakeFiles/bocopwrapper.dir/CMakeFiles/bocopwrapper.dir/bocopwrapperPYTHON_wrap.cxx.o
> [ 53%] Linking CXX shared module /opt/ct-gallery/gallery/examples/bistable/_bocopwrapper.so
> -- Moving python modules to /opt/ct-gallery/gallery/examples/bistable
> [ 53%] Built target bocopwrapper
> Scanning dependencies of target bocopApp
> [ 57%] Building CXX object src/CMakeFiles/bocopApp.dir/AD/dOCPCppAD.cpp.o
> [ 60%] Building CXX object src/CMakeFiles/bocopApp.dir/DOCP/dOCP.cpp.o
> [ 64%] Building CXX object src/CMakeFiles/bocopApp.dir/DOCP/dODE.cpp.o
> [ 67%] Building CXX object src/CMakeFiles/bocopApp.dir/DOCP/dControl.cpp.o
> [ 71%] Building CXX object src/CMakeFiles/bocopApp.dir/DOCP/dState.cpp.o
> [ 75%] Building CXX object src/CMakeFiles/bocopApp.dir/DOCP/solution.cpp.o
> [ 78%] Building CXX object src/CMakeFiles/bocopApp.dir/NLP/NLPSolverIpopt.cpp.o
> [ 82%] Building CXX object src/CMakeFiles/bocopApp.dir/OCP/OCP.cpp.o
> [ 85%] Building CXX object src/CMakeFiles/bocopApp.dir/tools/tools.cpp.o
> [ 89%] Building CXX object src/CMakeFiles/bocopApp.dir/tools/tools_interpolation.cpp.o
> [ 92%] Building CXX object src/CMakeFiles/bocopApp.dir/opt/ct-gallery/gallery/examples/bistable/problem.cpp.o
> [ 96%] Building CXX object src/CMakeFiles/bocopApp.dir/main.cpp.o
> [100%] Linking CXX executable /opt/ct-gallery/gallery/examples/bistable/bocopApp
> [100%] Built target bocopApp
[DONE] > make
Done
[3]:
0
State 0 and State 1 correspond to \(x_1\) and \(x_2\) respectively. State 2 represents the final time to minimize.
[4]:
import matplotlib.pyplot as plt
bocop.run(problem_path)
plt.show()
Done
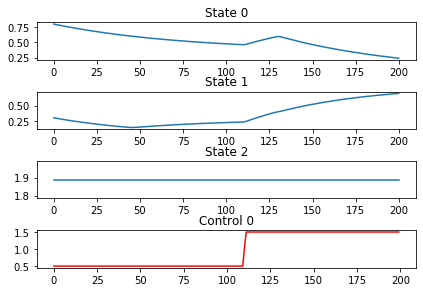
[5]:
import numpy as np
solution = bocop.readSolution(problem_path + "/problem.sol")
tf = solution.state[2][0]; t = solution.time_steps*tf
x1 = solution.state[0]; x2 = solution.state[1]
u = solution.control[0]
umin = 0.5
umax = 1.5
g1 = 1.4
g2 = 1.8
theta1 = 0.6
theta2 = 0.4
k1 = 1
k2 = 1
x1max = 0.9
x2max = 0.8
plt.figure(0, figsize=(10,4))
plt.subplots_adjust(hspace=0.4, wspace=0.4)
plt.subplot(121)
ax = plt.gca()
plt.xlabel('$x_1$'); plt.ylabel('$x_2$')
ax.set_ylim(0.,x1max); ax.set_xlim(0.,x2max)
xv = np.arange(0,theta1,0.01)
sumax = k2/g2*umax - (k2/g2*umax - theta2)*((k1/g1*umax - xv)/((k1/g1*umax - theta1)))**(g2/g1)
plt.plot(x1,x2,label='',zorder=3)
plt.plot(xv,sumax,'--', label='$(S_{u_{max}})$',linewidth=1, color='grey')
plt.legend()
plt.xlim([0,theta1*1.8])
ax.text(x1[0]+0.04, x2[0]-0.05, '$(x_1^0, x_2^0)$')
plt.scatter([x1[0],x1[-1]],[x2[0],x2[-1]], zorder=3, s=20)
plt.xticks([0, theta1], [0,'$\\theta_1$'])
plt.yticks([0, theta2, x2[-1]], [0,'$\\theta_2$','$x_2^f$'])
plt.grid(linestyle='dotted')
plt.subplot(122)
plt.plot(t[1:],u)
plt.xlabel('Time'); plt.ylabel('$u$')
plt.yticks([umin,1,umax], ['$u_{min}$', 1, '$u_{max}$'])
plt.grid(linestyle='dotted')
plt.show()
print("Final time is " + str(tf))
Loading solution: ./problem.sol
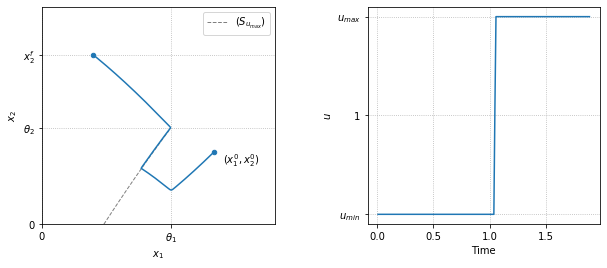
Final time is 1.88756560904673
[6]:
print("Bocop returns status {} with objective {:2.4g} and constraint violation {:2.4g}".format(solution.status,solution.objective,solution.constraints))
p0 = []
for i in range(solution.dim_state):
p0.append(solution.costate[i][0])
print("Costate at first time stage (t0+h/2): ",p0)
print("Multipliers for initial conditions: ",solution.boundarycond_multipliers[0:solution.dim_state])
Bocop returns status 0 with objective 1.888 and constraint violation 1.486e-14
Costate at first time stage (t0+h/2): [-2.21241861069235, 0.680215961376846, 0.99503700918767]
Multipliers for initial conditions: [-2.18337787e+00 6.68757718e-01 1.38521948e-12]