Notebook source code:
examples/geometry2D/skeleton/skeleton.ipynb
Run the notebook yourself on binder

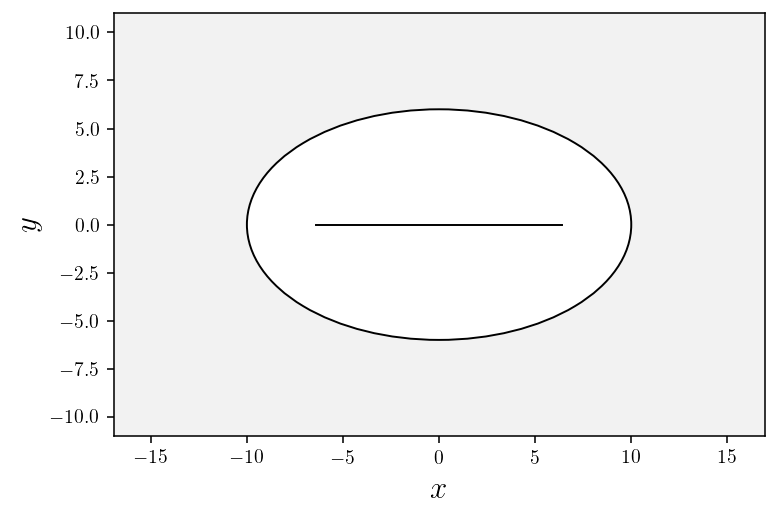
Skeleton of an ellipse¶
Preliminaries¶
Packages¶
[1]:
import numpy as np
import nutopy as nt
import os
import json
import matplotlib.pyplot as plt
import matplotlib.patches as patches
plt.rcParams['figure.dpi'] = 140
plt.rcParams.update({"text.usetex":True, "font.family":"sans-serif", "font.sans-serif":["Helvetica"]})
Hamiltonian: compilation of Fortran code¶
The Hamiltonian is
[2]:
# Fortran Hamiltonian code
!pygmentize hfun.f90
subroutine hfun(x, p, h)
double precision, intent(in) :: x(2), p(2)
double precision, intent(out) :: h
h = 0.5d0 * (p(1)**2 + p(2)**2)
end subroutine hfun
[3]:
# Compilation of the hamiltonian and associated derivatives up to order 3
!python -m numpy.f2py -c hfun.f90 -m hfun > /dev/null 2>&1
!python -m numpy.f2py -c hfun_d.f90 -m hfun_d > /dev/null 2>&1
!python -m numpy.f2py -c hfun_d_d.f90 -m hfun_d_d > /dev/null 2>&1
!python -m numpy.f2py -c hfun_d_d_d.f90 -m hfun_d_d_d > /dev/null 2>&1
from hfun import hfun as hf
from hfun_d import hfun_d as hf_d
from hfun_d_d import hfun_d_d as hf_d_d
from hfun_d_d_d import hfun_d_d_d as hf_d_d_d
[ ]:
# parameterization of initial state and costate
!python -m numpy.f2py -c point.f90 curve_d.f90 -m point > /dev/null 2>&1
!python -m numpy.f2py -c point_d.f90 -m point_d > /dev/null 2>&1
!python -m numpy.f2py -c point_d_d.f90 -m point_d_d > /dev/null 2>&1
from point import point as ip
from point_d import point_d as ip_d
from point_d_d import point_d_d as ip_d_d
Initialization¶
[5]:
datafile = "data.json"
def savedata(d):
file = open(datafile, "w")
json.dump(d,file)
file.close()
# Parameters
restart = False
if os.path.isfile(datafile) and not(restart):
file = open(datafile, "r")
data = json.load(file)
t0 = data.get('t0')
r1 = data.get('r1')
r2 = data.get('r2')
print('data loaded')
else:
# radius
r1 = 10.0
r2 = 6.0
# initial time
t0 = 0.0
# Data
data = {'t0': t0, 'r1': r1, 'r2': r2}
# Save data
savedata(data)
print('data saved')
data loaded
Hamiltonian flow and the exponential mapping¶
From the Hamiltonian \(H\), we define the Hamiltonian system
The exponential mapping \(\exp(t \vec{H})\) is then defined by
where \(z(t_f, t_0, x_0, p_0)\) is the solution at time \(t_f\) of the Cauchy problem
[6]:
# Hamiltonian and derivatives
hfun = lambda t, x, p : hf(x, p)
dhfun = lambda t, x, dx, p, dp : hf_d(x, dx, p, dp)
d2hfun = lambda t, x, dx, d2x, p, dp, d2p : hf_d_d(x, d2x, dx, p, d2p, dp)
d3hfun = lambda t, x, dx, d2x, d3x, p, dp, d2p, d3p : hf_d_d_d(x, d3x, d2x, dx, p, d3p, d2p, dp)
hfun = nt.tools.tensorize(dhfun, d2hfun, d3hfun, tvars=(2, 3), full=True)(hfun)
h = nt.ocp.Hamiltonian(hfun)
# Exponential mapping and its derivatives
exponential = nt.ocp.Flow(h)
Parameterization of the initial covector¶
By homogeneity, we can fix \(H = 1/2\) and that is we fix \(||p_0||=1\).
[7]:
# Initial state-costate parameterization and derivatives
initial_point = lambda alpha : ip(alpha)
dinitial_point = lambda alpha, dalpha : ip_d(alpha, dalpha)
d2initial_point = lambda alpha, dalpha, d2alpha : ip_d_d(alpha, d2alpha, dalpha)
initial_point = nt.tools.tensorize(dinitial_point, d2initial_point, tvars=(1,), full=True)(initial_point)
Geodesics¶
A geodesic is the projection of an extremal given by the exponential mapping. That is
where \(\pi_q(q, p) = q\) is the canonical projection on the state space.
[8]:
# Compute a geodesic parameterized by alpha to time t
def geodesic(t, alpha):
N = 100
tspan = list(np.linspace(t0, t, N+1))
q0, p0 = initial_point(alpha)
q, p = exponential(t0, q0, p0, tspan)
return q
[9]:
# Initial plotting
def plotInitFig():
# 2D
fig = plt.figure()
ax = fig.add_subplot(111)
r = 2*r1
x = [-r, r, r, -r]
y = [-r, -r, r, r]
ax.fill(x, y, color=(0.95, 0.95, 0.95))
circle = patches.Ellipse((0,0), 2.*r1, 2.*r2, ec="black", fc='white')
ax.add_patch(circle)
ax.set_xlabel(r'$x$', fontsize=16)
ax.set_ylabel(r'$y$', fontsize=16)
ax.axis('equal')
plt.xlim(-1.1*r1, 1.1*r1);
plt.ylim(-1.1*r1, 1.1*r1);
ax2D = ax
return ax2D
# function to plot geodesics
def plotGeodesics(ax2d=None, nb_geodesics=15, tf=2.*r1):
if ax2d is None:
ax2d = plotInitFig()
alphas = np.linspace(0.0, 2.0*np.pi, nb_geodesics)
for alpha in alphas[0:-1]:
q = np.array(geodesic(tf, alpha))
ax2d.plot(q[:,0], q[:,1], color='b', linewidth=0.5)
return ax2d
[10]:
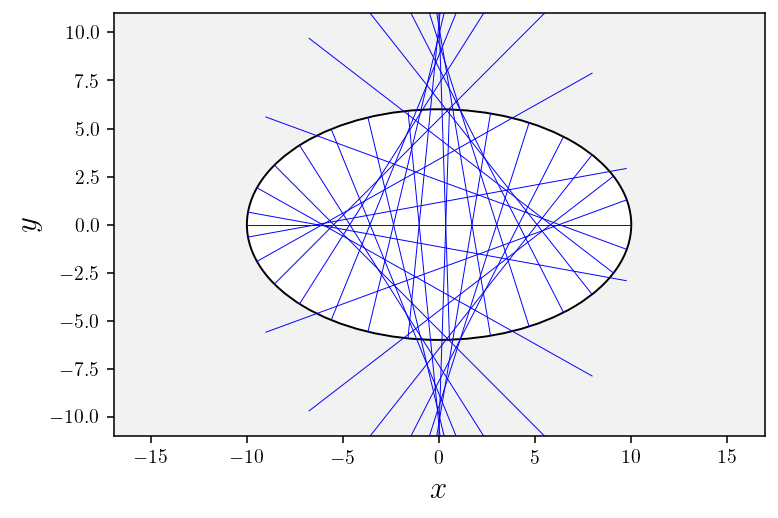
# Plot geodesics
plotGeodesics(nb_geodesics=30);
Conjugate locus¶
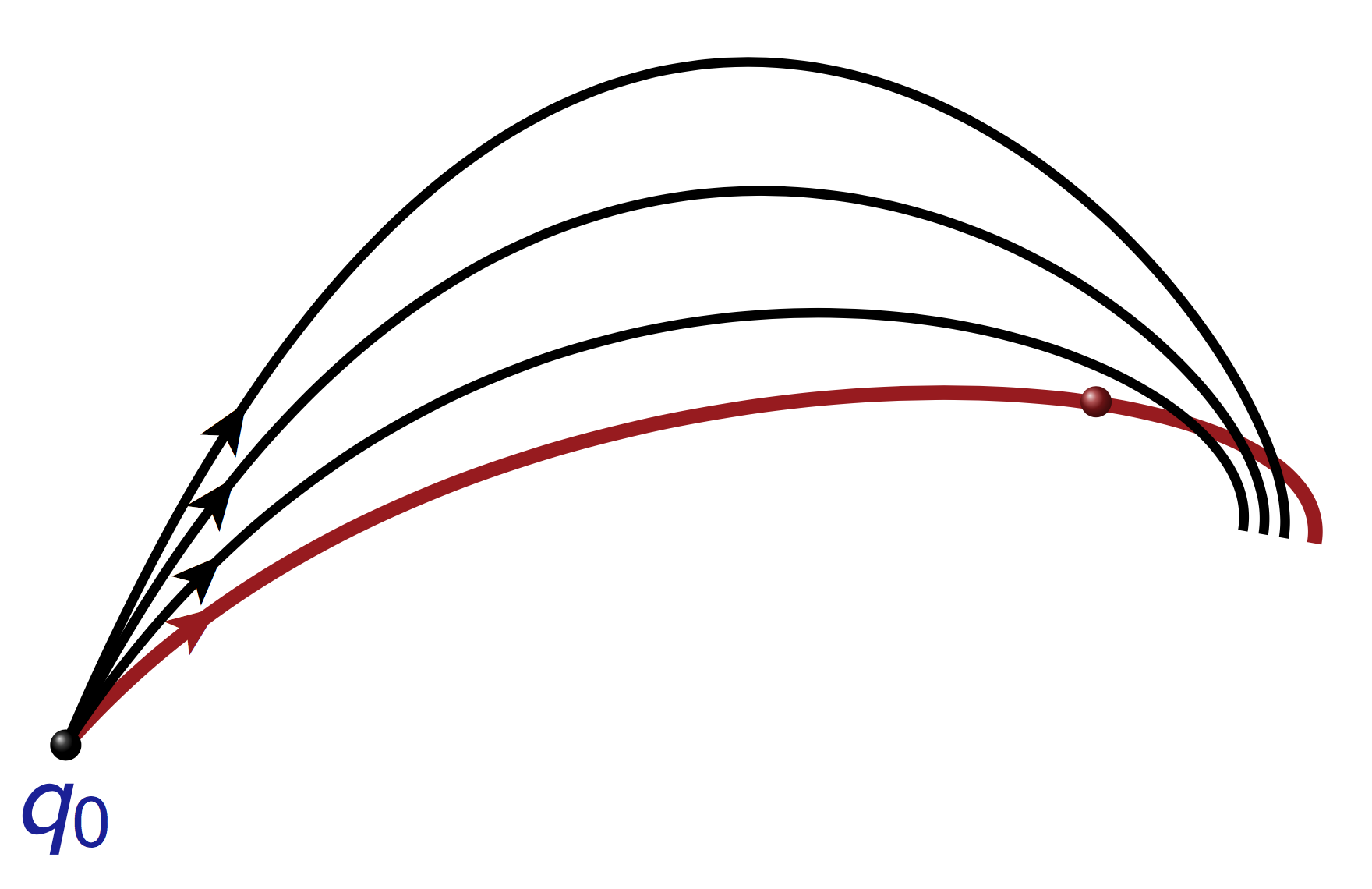
Jacobi fields¶
A Jacobi field is a solution of the variational equation of the exponential mapping.
[11]:
# Canonical first projection of the Jacobi field: dq(t, p0(alpha), dp0(alpha)),
# with J = (dq, dp) the Jacobi field
@nt.tools.vectorize(vvars=(1,))
def jacobi(t, alpha):
q0, dq0, p0, dp0 = initial_point((alpha, 1.))
(q, dq), _ = exponential(t0, (q0, dq0), (p0, dp0), t)
return dq
[12]:
# Derivative of jacobi
def djacobi(t, alpha):
q0, dq0, d2q0, p0, dp0, d2p0 = initial_point ((alpha, 1., 1.))
(q, dq1, d2q), (p, dp1, _) = exponential(t0, (q0, dq0, dq0), (p0, dp0, dp0), t)
(q, dq2), (p, dp2) = exponential(t0, (q0, d2q0), (p0, d2p0), t)
# djacobi/dalpha
djda = d2q+dq2
# djacobi/dt
hv, dhv = h.vec(t, (q, dq1), (p, dp1))
djdt = dhv[0:2]
return djdt, djda
Equation for the calculation of conjugate points¶
| Let \(q\) being a reference geodesic and \(J := (\delta q, \delta p)\) the associated Jacobi field. A conjugate time \(t_c\) along \(q\) is a solution of the equation
\[t \mapsto \det \left(\dot{q}(t), \delta q(t) \right).\]
A conjugate point is the associated point: \(q(t_c)\). |
[13]:
# conjugate(t, q, a) = ( det(jacobi(t, a), Hv(t, z(t, a))), q - pi_q(z(t, a)) ),
# where pi_q(q, p) = q and z(t, a) = exponential(t0, q0, p0(q0, a), t).
#
# Remark: y = (t, q)
#
def conjugate(y, a):
t = y[0]
q = y[1:3]
alpha = a[0]
#
dq = jacobi(t, alpha)
#
q0, p0 = initial_point(alpha)
qt, pt = exponential(t0, q0, p0, t)
hv = h.vec(t, qt, pt)[0:2]
#
c = np.zeros(3)
c[0] = np.linalg.det([hv, dq])
c[1:3] = q - qt
return c
[14]:
# Derivative of conjugate
def dconjugate(y, a):
t = y[0]
x = y[1:3]
alpha = a[0]
#
dx = jacobi(t, alpha)
#
ddxdt, ddxda = djacobi(t, alpha)
#
q0, dq0, p0, dp0 = initial_point((alpha, 1.))
(xf, dxf), (pf, dpf) = exponential(t0, (q0, dq0), (p0, dp0), t)
hv, dhv = h.vec(t, (xf, dxf), (pf, dpf))
#
# dc/da
dcda = np.zeros((3, 1))
dcda[0,0] = np.linalg.det([dhv[0:2], dx])+np.linalg.det([hv[0:2], ddxda])
dcda[1:3,0] = -dxf
#
# dc/dy = (dc/dt, dc/dx)
hv, dhv = h.vec(t, (xf, hv[0:2]), (pf, hv[2:4]))
dcdy = np.zeros((3, 3))
dcdy[0,0] = np.linalg.det([dhv[0:2], dx])+np.linalg.det([hv[0:2], ddxdt])
dcdy[1:3,0] = -hv[0:2]
dcdy[1,1] = 1.
dcdy[2,2] = 1.
return dcdy, dcda
Conjugate locus¶
[15]:
def get_conjugate_locus():
# -------------------------
# Get first conjugate point
# Initial guess
gap = 1e-2
tci = np.pi
alpha = np.array([-np.pi/2+gap])
q0, p0 = initial_point(float(alpha))
xi, pi = exponential(t0, q0, p0, tci)
yi = np.zeros(3)
yi[0] = tci
yi[1:3] = xi
# Equations and derivative
fun = lambda t: conjugate(t, alpha)
dfun = lambda t: dconjugate(t, alpha)[0]
# callback
def print_conjugate_time(infos):
print(' Conjugate time estimation: tc = %e for alpha = %e' % (infos.x[0], alpha), end='\r')
# Options
opt = nt.nle.Options(Display='off')
# Conjugate point calculation
print(' > Get first conjugate time and point:\n')
sol = nt.nle.solve(fun, yi, df=dfun, callback=print_conjugate_time, options=opt)
# -------------------
# Get conjugate locus
# options
opt = nt.path.Options(MaxStepSizeHomPar=0.05, Display='off');
# homotopic parameter range
alpha0 = alpha
alphaf = np.pi/2.-gap
# initial solution
y0 = sol.x
# callback
def progress(infos):
current = float(infos.pars)-alpha0
total = alphaf-alpha0
barLength = 50
percent = float(current * 100.0 / total)
arrow = '-' * int(percent/100 * barLength - 1) + '>'
spaces = ' ' * (barLength - len(arrow))
print(' Progress: [%s%s] %1.2f %%' % (arrow, spaces, round(percent, 2)), end='\r')
# Conjugate locus calculation
print('\n\n > Get conjugate locus:\n')
sol = nt.path.solve(conjugate, y0, alpha0, alphaf, options=opt, df=dconjugate, callback=progress)
print('\n')
return sol.xout
# Plot conjugate locus
def plotConjugateLocus(conjugate_locus, ax2d=None):
if ax2d is None:
ax2d = plotInitFig()
#
ax2d.plot( conjugate_locus[:,1], conjugate_locus[:,2], color='r', linewidth=1.0)
ax2d.plot( -conjugate_locus[:,1], conjugate_locus[:,2], color='r', linewidth=1.0)
return ax2d
[16]:
# Get conjugate locus
if 'conjugate_locus' in data.keys():
conjugate_locus = np.array(data.get('conjugate_locus'))
print('Conjugate locus loaded')
else:
conjugate_locus = get_conjugate_locus()
data['conjugate_locus'] = conjugate_locus.tolist()
savedata(data)
print('Conjugate locus saved')
Conjugate locus loaded
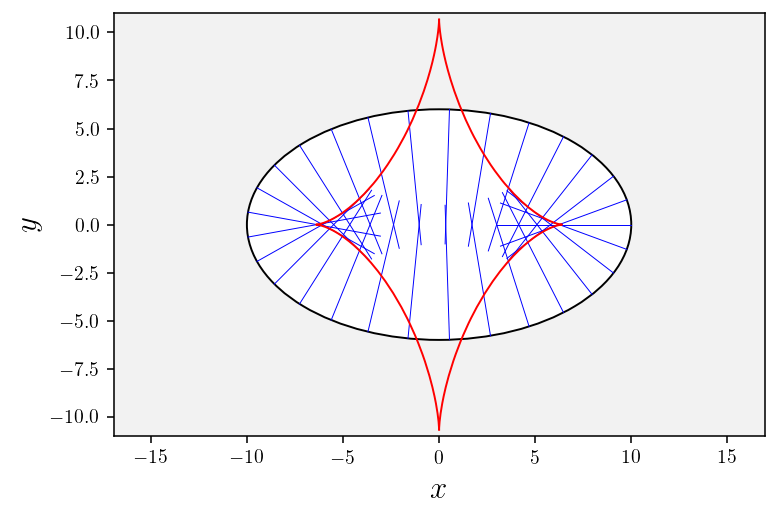
[17]:
# Plot geodesics
ax2d = plotGeodesics(nb_geodesics=30, tf=7.)
# Plot conjugate locus
plotConjugateLocus(conjugate_locus, ax2d);
Wavefronts¶
The wavefront at time \(t\) is simply given by
[18]:
# Equation to calculate wavefronts
def wavefront_eq(q, alpha, tf):
q0, p0 = initial_point(float(alpha))
qf, _ = exponential(t0, q0, p0, tf)
return q - qf
[19]:
# Derivative
def dwavefront_eq(q, dq, alpha, dalpha, tf):
q0, dq0, p0, dp0 = initial_point((float(alpha), float(dalpha)))
(qf, dqf), _ = exponential(t0, (q0, dq0), (p0, dp0), tf)
return q - qf, dq - dqf
wavefront_eq = nt.tools.tensorize(dwavefront_eq, tvars=(1, 2), full=True)(wavefront_eq)
[20]:
def get_wavefront(tf):
# Options
opt = nt.path.Options(Display='off', MaxStepSizeHomPar=0.1, MaxIterCorrection=0);
# Homotopic parameter range
alpha0 = 0.0
alphaf = 2.0*np.pi
# Initial solution
q0, p0 = initial_point(alpha0)
xf0, _ = exponential(t0, q0, p0, tf)
# callback
def progress(infos):
current = float(infos.pars)-alpha0
total = alphaf-alpha0
barLength = 50
percent = float(current * 100.0 / total)
arrow = '-' * int(percent/100.0 * barLength - 1) + '>'
spaces = ' ' * (barLength - len(arrow))
print(' Progress: [%s%s] %1.2f %%' % (arrow, spaces, round(percent, 2)), end='\r')
# wavefront computation
print('\n > Get wavefront for tf =', tf, '\n')
# sol = nt.path.solve(wavefront_eq, xf0, alpha0, alphaf, args=tf, options=opt, callback=progress)
sol = nt.path.solve(wavefront_eq, xf0, alpha0, alphaf, args=tf, options=opt, df=wavefront_eq, callback=progress)
print('\n')
wavefront = (sol.xout, sol.parsout, tf)
return wavefront
[21]:
def plotWavefront(wavefront, ax2d=None):
if ax2d is None:
ax2d = plotInitFig()
#
ax2d.plot( wavefront[:,0], wavefront[:,1], color='g', linewidth=1.0)
return ax2d
[22]:
# Calculate wavefront
if 'wavefronts' in data.keys():
wavefronts = data.get('wavefronts')
print('Wavefronts loaded')
else:
wavefronts = []
wavefront = get_wavefront(tf=2.0); wavefronts.append((wavefront[0].tolist(), wavefront[1].tolist(), wavefront[2]))
wavefront = get_wavefront(tf=5.5); wavefronts.append((wavefront[0].tolist(), wavefront[1].tolist(), wavefront[2]))
data['wavefronts'] = wavefronts
savedata(data)
print('Wavefronts saved')
Wavefronts loaded
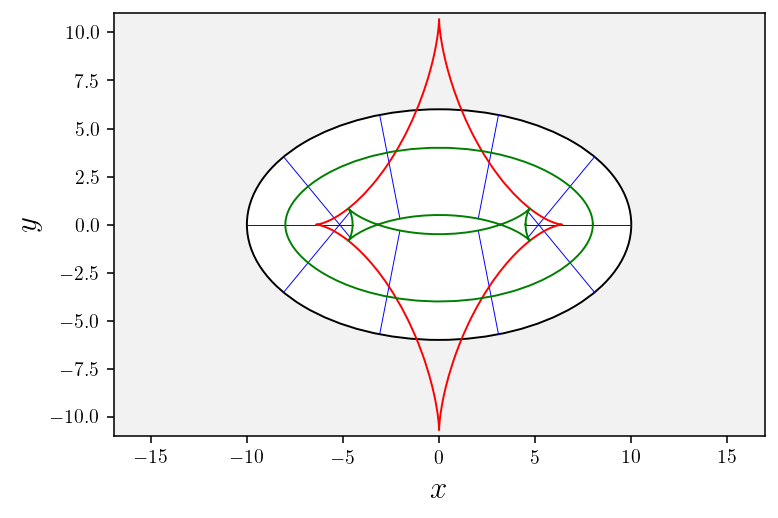
[23]:
# Plot geodesics
ax2d = plotGeodesics(nb_geodesics=11, tf=5.5)
# Plot conjugate locus
plotConjugateLocus(conjugate_locus, ax2d)
# Plot wavefronts
for w in wavefronts:
wavefront = np.array(w[0]); plotWavefront(wavefront, ax2d);
Cut locus¶
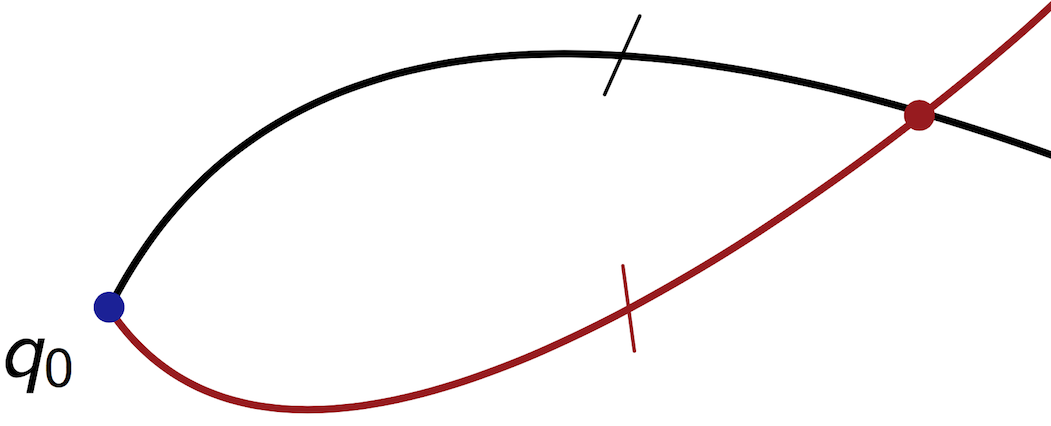
We call a splitting point a point where two minimizing geodesics intesect. In the Riemanian case, this corresponds to self-intersection of the wavefront.
We call a cut point along a reference geodesic the point where this geodesic loses its optimality.
We have that a cut point is either a conjugate point or a splitting point.
|
|
Splitting point | Conjugate point |
Self-intersection of the wavefront¶
[24]:
def get_self_intersection(curve):
n = curve[:,0].size
intersections = []
for i in range(n-3):
A = curve[i,:]
B = curve[i+1,:]
for j in range(i+2,n-1):
C = curve[j,:]
D = curve[j+1,:]
# Matrice M : M z = b
m11 = B[0] - A[0]
m12 = C[0] - D[0]
m21 = B[1] - A[1]
m22 = C[1] - D[1]
det = m11*m22-m12*m21
if(np.abs(det)>1e-8):
b1 = C[0] - A[0]
b2 = C[1] - A[1]
la = (m22*b1-m12*b2)/det
mu = (m11*b2-m21*b1)/det
if(la>=0. and la<=1. and mu>=0. and mu<=1.):
xx = {'i': i, 'j': j, 'x': np.array(A + la * (B-A)), 'la': la, 'mu': mu}
intersections.append(xx)
return intersections
[25]:
wa = wavefronts[-1]
wavefront = np.array(wa[0])
alphas = np.array(wa[1])
tf = wa[2]
xxs = get_self_intersection(wavefront)
xx = xxs[0]
x = xx.get('x')
i = xx.get('i')
j = xx.get('j')
la = xx.get('la')
mu = xx.get('mu')
alpha1 = alphas[i]+la*(alphas[i+1]-alphas[i])
alpha2 = alphas[j]+mu*(alphas[j+1]-alphas[j])
print('Self-intersection of the wavefront for tf =', tf, 'at x = (', x[0], ',', x[1], ')\n')
print('alpha1 =', alpha1)
print('alpha2 = ', alpha2)
Self-intersection of the wavefront for tf = 5.5 at x = ( 3.1965134103212356 , -3.283815059361428e-05 )
alpha1 = 1.0477472419890679
alpha2 = 5.235416311093603
[26]:
# Equations to calculate splitting locus
def split_eq(y, alpha):
# y = (q, a, t)
q = y[0:2]
a = y[2]
t = y[3]
b = float(alpha)
q0, p0 = initial_point(a)
q1, _ = exponential(t0, q0, p0, t)
q0, p0 = initial_point(b)
q2, _ = exponential(t0, q0, p0, t)
eq = np.zeros(4)
eq[0:2] = q-q1
eq[2:4] = q1-q2
return eq
[27]:
# Derivative
def dsplit_eq(y, dy, alpha, dalpha):
x = y[0:2]
a = y[2]
t = y[3]
dx = dy[0:2]
da = dy[2]
dt = dy[3]
b = float(alpha)
db = float(dalpha)
q0, dq0, p0, dp0 = initial_point((a, da))
(x1, dx1), _ = exponential(t0, (q0, dq0), (p0, dp0), (t, dt))
q0, dq0, p0, dp0 = initial_point((b, db))
(x2, dx2), _ = exponential(t0, (q0, dq0), (p0, dp0), (t, dt))
deq = np.zeros(4)
deq[0:2] = dx-dx1
deq[2:4] = dx1-dx2
return deq
split_eq = nt.tools.tensorize(dsplit_eq, tvars=(1, 2))(split_eq)
[28]:
def get_splitting_locus(q, a, t, b):
# Options
opt = nt.path.Options(Display='off', MaxStepSizeHomPar=0.1, MaxIterCorrection=7);
# Homotopic parameter range
epsi = 1e-2
alpha0 = np.pi+epsi
alphaf = 2.0*np.pi-epsi
# Initial solution
y0 = np.array([q[0], q[1], a, t])
b0 = b
# callback
def progress_bis(infos):
current = b0-float(infos.pars)
total = alphaf-alpha0+b0-alpha0
barLength = 50
percent = float(current * 100.0 / total)
arrow = '-' * int(percent/100.0 * barLength - 1) + '>'
spaces = ' ' * (barLength - len(arrow))
print(' Progress: [%s%s] %1.2f %%' % (arrow, spaces, round(percent, 2)), end='\r')
# First homotopy
print('\n > Get splitting locus\n')
sol = nt.path.solve(split_eq, y0, b0, alpha0, options=opt, df=split_eq, callback=progress_bis)
ysol = sol.xf
# callback
def progress(infos):
current = b0-float(infos.pars)+float(infos.pars)-alpha0
total = alphaf-alpha0+b0-alpha0
barLength = 50
percent = float(current * 100.0 / total)
arrow = '-' * int(percent/100.0 * barLength - 1) + '>'
spaces = ' ' * (barLength - len(arrow))
print(' Progress: [%s%s] %1.2f %%' % (arrow, spaces, round(percent, 2)), end='\r')
# splitting computation
sol = nt.path.solve(split_eq, ysol, alpha0, alphaf, options=opt, df=split_eq, callback=progress)
print('\n')
splitting_locus = sol.xout
return splitting_locus
[29]:
def plotSplitting(splitting_locus, ax2d=None):
if ax2d is None:
ax2d = plotInitFig()
#
ax2d.plot( splitting_locus[:,0], splitting_locus[:,1], color='k', linewidth=1)
return ax2d
[30]:
# Get splitting locus
if 'splitting_locus' in data.keys():
splitting_locus = np.array(data.get('splitting_locus'))
print('Splitting locus loaded')
else:
splitting_locus = get_splitting_locus(x, alpha1, tf, alpha2)
data['splitting_locus'] = splitting_locus.tolist()
savedata(data)
print('Splitting locus saved')
Splitting locus loaded
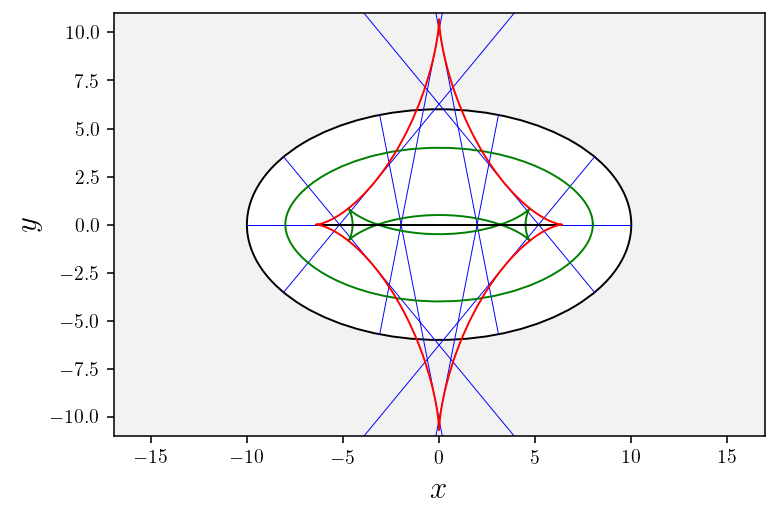
[31]:
# Plot geodesics
ax2d = plotGeodesics(nb_geodesics=11)
# Plot wavefronts
for w in wavefronts:
wavefront = np.array(w[0]); plotWavefront(wavefront, ax2d)
# plot splitting locus
plotSplitting(splitting_locus, ax2d)
# Plot conjugate locus
plotConjugateLocus(conjugate_locus, ax2d);
[32]:
# plot splitting locus
plotSplitting(splitting_locus);